Oscillateur Harmonique libre non-amorti
Dans cet article, nous allons traiter des vibrations harmoniques libres non-amorties. Concrètement, nous allons considérer une masse 
attaché à un mur par un ressort dont la constante de raideur est notée 
.
Le qualificatif « non-amorti » signifie que nous allons négliger les forces de frottement. Ainsi, le poids et la réaction du support (opposée au poids) sont les seules forces que nous considéreront, en plus de la froce de rappel du ressort.
Le qualificatif « libre », quant à lui, signifie qu’aucune autre force que celles sus-citées ne vient exciter l’oscillateur.
Bilan des forces:
– Poids : 
– Réaction du support : 
– Force de rappel: 
En faisant le bilan des forces, on constate que 
et 
sont opposées et de même norme. Par conséquent, le mouvement s’effectue uniquement selon l’axe 
.
Remarque:
On notera le terme 
dans l’expression de la force de rappel. Il s’agit de l’écart de la masse par rapport à la position d’équilibre. Communément, si 
est la position d’équilibre, on aura alors 
où 
est l’abscisse de la masse.
On notera par ailleurs que 
.
On peut dès à présent écrire l’équation du mouvement (seconde loi de Newton):
(1) 
Ainsi, on obtient l’équation suivante:
(2) 
On introduit alors une constante 
appelée « pulsation » définie de la manière suivante:
(3) 
On peut vérifier que a la dimension d’une pulsation (ou d’une fréquence). Notre équation (2) peut alors se ré-écrire sous la forme suivante:
(4) 
La solution de cette équation est immédiate:
(5) 
Les constantes 
et 
dépendent des conditions initiales.
Remarque:
On notera que l’on peut tout aussi bien écrire 
, où 
et 
sont elles aussi deux constantes dépendant des conditions initiales.
On notera que l’on peut également utiliser la représentation complexe, à savoir 
où et sont cette fois ci des nombre sa priori complexes, 
devant demeurer réel.
Enfin, on peut définir la fréquence des oscillations 
ainsi que la période 
.
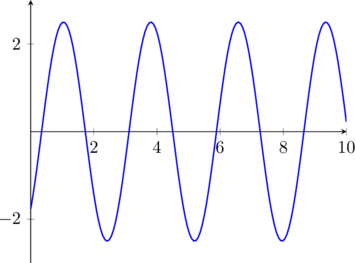
Sur le graphique ci-dessus, on peut voir l’allure de la courbe associée à avec des conditions initiales et une pulsation particulières.
Conclusion:
En analysant la forme de la solutions, on constate que la position (ou plutôt l’écart à la position d’équilibre) de la masse est décrite par une fonction périodique, de période . La masse va donc osciller à l’infini dans cette configuration, tant qu’elle ne sera pas perturbée par une force extérieure, c’est pourquoi elle est « libre ». En outre, la période 
des oscillations dépend uniquement de la masse et de la raideur du ressort.
