Formule de Stirling
La formule de Stirling est célèbre pour donner une très bonne approximation de la factorielle d’un nombre. En effet, elle se révèle extrêmement efficace, avec une erreur inférieur à 2% dès le cinquième rang. On rappelle la formule ci-dessous:
![\[ n! \sim \sqrt{2\pi n}\left(\dfrac{n}{e}\right)^n \]](https://www.leotheodon.com/V4/wp-content/ql-cache/quicklatex.com-165b6c570554f0b295f0754182d890ce_l3.png "Rendered by QuickLaTeX.com")
Nous allons donner l’idée d’une démonstration utilisant la méthode du col.
Démonstration:
Exprimons tout d’abord la factorielle à l’aide de la fonction Gamma d’Euler:
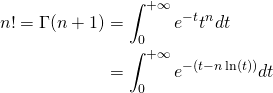
On note 
. On peut remarquer que cette fonction admet un minimum en calculant sa dérivée.
(1) 
On remarque que l’on a 
. Ainsi, la fonction 
admet un minimum en 
.
On peut alors écrire le développement de Taylor de au voisinage de 
sous la forme suivante:
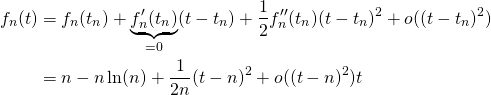
Ainsi, on peut écrire:
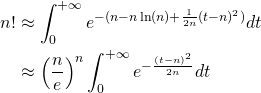
En effectuant le changement de variable 
et 
, on obtient:
(2) 
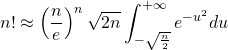
De plus, pour 
suffisamment grand, on a:
(3) 
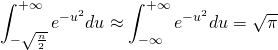
Ainsi, on en déduit la formule de Stirling:
(4) 
Remarque:
On pourra noter que la démonstration ci-dessus n’est pas complètement rigoureuse. Les notations sont lacunaires (il faudrait préciser les passages à la limite et les équivalents à l’infini), et on passe rapidement sur l’utilisation du développement de Taylor. Pour s’en convaincre, on peut regarder l’allure de la courbe associée à la fonction 
.
