Diffraction de rayons X par un cristal
On considère un cristal éclairé par un rayonnement X incident caractérisé par une onde plane monochromatique, de vecteur d’onde 
et d’amplitude 
. Le facteur de diffusion atomique 
d’un élément chimique 
est défini par 
. Dans la suite, on considèrera que la diffusion est élastique de sorte que la diffraction par le cristal se ramène à l’étude d’interférence entre les ondes planes monochromatiques diffusées par les atomes de la structure cristalline.
Déphasage entre deux ondes diffusées :
On considère deux atomes situés en 
et 
, interagissant avec l’onde incident de vecteur d’onde et émettant chacun une onde de vecteur d’onde 
.
Sur le schéma ci-contre, on a:
La différence de marche est donc égale à 
.
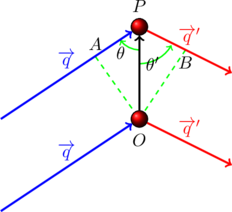
La différence de marche entre les deux ondes diffusées par et est 
. On a alors la relation suivante:
(1) 
Or, on sait que 
où 
est la longueur d’onde. On en déduit l’expression du déphasage:
(2) 
On note 
.
Diffraction par un cristal parfait :
On considère un cristal caractérisé par un motif contenant 
atomes, dont les positions sont déterminées par 
, où les 
forment une base adaptée au réseau de Bravais, les 
sont des coefficients entiers, et 
, 
et 
sont des coefficients réels. Le cristal est de dimension 
pour 
. L’amplitude totale diffractée par le cristal est la somme des amplitudes des ondes émises par chaque atome du cristal.
(3) 
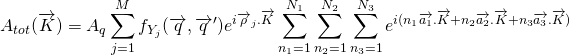
On rappelle que l’intensité totale est 
. D’après ce qui précède, on voit que l’intensité totale peut s’écrire sous la forme suivante:
(4) 
En effet, dans l’expression de l’amplitude, le premier facteur caractérise le motif, et on peut donc poser:
(5) 
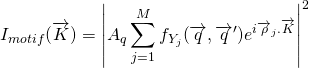
De plus, l’autre membre de l’expression de l’amplitude dépend uniquement du réseau de Bravais. On écrira alors:
(6) 
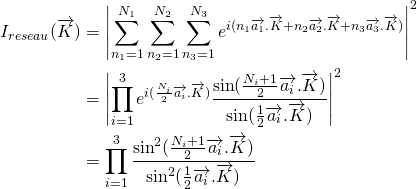
On en déduit alors immédiatement que l’intensité est maximale lorsque 
, avec 
(condition de Laue). En particulier, cette condition peut s’écrire sous la forme suivante:
(7) 
Conclusion :
Ce dernier résultat signifie que l’intensité est maximale lorsque 
appartient au réseau réciproque du cristal. De plus, on retrouve bien le fait que l’intensité est maximale lorsque 
(c’est-à-dire que l’on observe l’onde en sortie du cristal dans la même direction que l’onde incidente).
