Invariance d’un réseau de Bravais par rotation
Le but de cet exercice est de montrer que les rotations laissant invariant le réseau de Bravais d’un cristal ont des angles ![]() dont les seules valeurs possibles sont
dont les seules valeurs possibles sont ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() .
.
Démonstration :
Commençons par rappeler la forme de la matrice ![]() associée à une rotation d’angle
associée à une rotation d’angle ![]() dans un repère orthonormé adapté de l’espace.
dans un repère orthonormé adapté de l’espace.
(1) 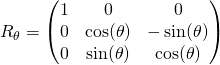
On note que la trace de cette matrice est ![]() . Ce résultat est important car la trace est invariante par changement de base.
. Ce résultat est important car la trace est invariante par changement de base.
Considérons à présent une base ![]() adapté au réseau de Bravais du cristal et notons
adapté au réseau de Bravais du cristal et notons ![]() la matrice de rotation précédente exprimée dans cette nouvelle base. Si le réseau est invariant par rotation d’angle
la matrice de rotation précédente exprimée dans cette nouvelle base. Si le réseau est invariant par rotation d’angle ![]() , alors on a
, alors on a ![]() , c’est-à-dire que la rotation entraîne une permutation des vecteur
, c’est-à-dire que la rotation entraîne une permutation des vecteur ![]() au signe près. Ainsi, si l’on écrit
au signe près. Ainsi, si l’on écrit ![]() dans la base des vecteur
dans la base des vecteur ![]() , on obtient une matrice dont les coefficients sont entiers, égaux à
, on obtient une matrice dont les coefficients sont entiers, égaux à ![]() , comme par exemple:
, comme par exemple:
(2) 
Dans tous les cas, le résultat qui nous importe est que la trace de la matrice ![]() est entière. Ainsi, on peut écrire la relation suivante:
est entière. Ainsi, on peut écrire la relation suivante:
(3) ![]()
On obtient alors immédiatement les valeurs de ![]() possibles,
possibles, ![]() étant forcément entier ou demi-entier, à savoir
étant forcément entier ou demi-entier, à savoir ![]() ,
, ![]() ,
, ![]() ,
, ![]() ou
ou ![]() .
.
Remarque :
Il vient alors comme conséquence immédiate, en observant les valeurs possible pour ![]() , que les seules rotations laissant invariantes le réseau de Bravais sont d’ordre
, que les seules rotations laissant invariantes le réseau de Bravais sont d’ordre ![]() ou
ou ![]() .
.


