Volume de l’hypersphère

par Leo · Publié 3 février 2019 · Mis à jour 3 février 2019

Une hypersphère est une sphère en $D$ dimensions. Elle généralise le concept de sphère que nous connaissons tous en dimension 3. L’idée est ici de donner une expression pour le volume $V_D$ d’une hypersphère de rayon $R$ dans un espace à $D$ dimensions.

Tout d’abord, on peut écrire que $V_D = C_D \times R^D$ , où $C_D$ est le volume de l’hypersphère unité (hypersphère de rayon $R=1$ ).

Remarque :
On en déduit immédiatement l’expression de $S_D$ , la surface de l’hypersphère de rayon $R$ . En dérivant l’expression précédente par rapport à $R$ , on obtient: $S_D = D.C_D.R^{D-1}$ .

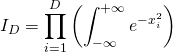Calculons à présent $C_D$ . Pour ce faire, nous allons poser $I_D = \displaystyle \prod_{i=1}^D \left( \int_{-\infty}^{+\infty} e^{-x_{i}^2} \right)$ . Tout d’abord, on peut remarquer que l’on a affaire à un produit d’intégrales de Gaussiennes. On a donc :

(1) $\begin{equation*} I_D = \displaystyle \prod_{i=1}^D \left( \int_{-\infty}^{+\infty} e^{-x_{i}^2} \right) = \prod_{i=1}^D \sqrt{\pi} = \sqrt{\pi}^D \end{equation*}$

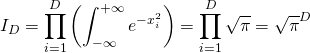
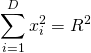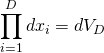Nous allons à présent effectuer le changement de variables $\displaystyle \sum_{i=1}^D x_{i}^2 = R^2$ et $\displaystyle \prod_{i=1}^D dx_i = dV_D$ . On peut dès lors écrire la relation suivante :

$\begin{align*} I_D = \displaystyle \prod_{i=1}^D \left( \int_{-\infty}^{+\infty} e^{-x_{i}^2} \right) & = \int_{-\infty}^{+\infty} e^{-(x_{1}^2+x_{2}^2+…+x_{D}^2)} dx_1dx_2…dx_D\\ & = \int_{0}^{+\infty} e^{-R^2}dV_D \end{align*}$

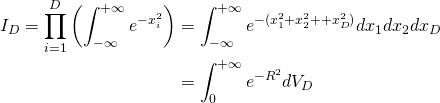
On peut alors effectuer le nouveau changement de variable $y=R^2$ . En particulier, on peut remarquer que l’on a la relation suivante :

(2) $\begin{equation*} dV_D = d(C_D.(R^2)^{\frac{D}{2}}) = d(C_D.(y)^{\frac{D}{2}}) = \dfrac{D}{2}C_Dy^{\frac{D}{2}-1}dy \end{equation*}$

On en déduit alors immédiatement la nouvelle expression de $I_D$ , c’est-à-dire :

(3) $\begin{align*} I_D & = \displaystyle \dfrac{D}{2}C_D \int_{0}^{+\infty} y^{\frac{D}{2}-1}e^{-y}dy\\& = \dfrac{D}{2}C_D \Gamma\left(\frac{D}{2}\right)\\& = \dfrac{D}{2}C_D \left(\frac{D}{2}-1\right)!\\& = C_D \left(\frac{D}{2}\right)! \end{align*}$

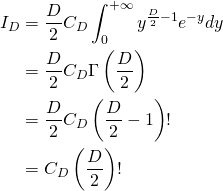
Ainsi, on obtient le volume de la sphère unité :

(4) $\begin{equation*} C_D = \dfrac{\sqrt{\pi}^D}{\left(\frac{D}{2}\right)!} \end{equation*}$

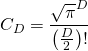
Ainsi, de manière générale, on a l’expression suivante pour le volume de l’hypersphère en dimension $D$ :

(5) $\begin{equation*}V_D = \dfrac{\sqrt{\pi}^D}{\left(\frac{D}{2}\right)!}R^D\end{equation*}$

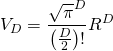
Remarque :
On remarquer que si l’on calcule le volume de l’hypersphère unité, ce dernier atteint un maximum pour $D=5$ . De plus, il est intéressant de voir que le volume de l’hypersphère tend vers 0 quand le nombre de dimension tend vers l’infini quand le volume de l’hypercube, quant à lui, égal à $2^D$ tend vers l’infini.