[Rapport] Statistique de Bose-Einstein

Introduction :
La physique statistique tend à émerger lors de la seconde moitié du XIXe siècle à partir de la théorie cinétique des gaz de Boltzmann, Maxwell, et bien d’autres. L’idée est d’expliquer les lois macroscopiques à partir d’études statistiques des comportements microscopiques.

Parmi les premiers résultats majeures obtenus à partir de cette nouvelle théorie, on peut citer notamment la capacité calorifique d’un gaz parfait, ou encore celle des solides où l’on peut retrouver la loi de Dulong-Petit à partir d’un calcul classique que mènera Boltzmann, expliquer pourquoi cette même loi n’est valide qu’à température ambiante pour la plupart des matériaux à l’aide du modèle d’Einstein ou encore le comportement aux très faibles températures à l’aide du modèle de Debye. On pourra également citer la loi de Planck permettant en particulier d’expliquer le rayonnement du corps noir.

Durant cette année de L3 – Physique fondamentale et application, nous avons été amenés à nous intéresser aux phénomènes sus-cités, ce travail aboutissant à la rédaction d’un rapport. Le programme est le suivant:

1. Développement autour du rayonnement du corps noir
   • Contexte historique et données expérimentales, limites du modèle classique
   • Introduction de la statistique de Bose-Einstein
   • Dérivation de la loi de Planck
2. Développement autour de la chaleur spécifique des solides
   • Définitions, position du problème et dérivation de la loi de Dulong-Petit sous des hypothèses classiques
   • Introduction du modèle d’Einstein
   • Introduction du modèle de Debye
3. Léger développement autour du phénomène de condensation de Bose-Einstein
   • Contexte historique et définition
   • Mise en évidence d’un température critique et du phénomène de condensation

La première partie sert principalement d’introduction et permet d’établir certains résultats de base de physique statistique. Quelques pré-requis sont nécessaires afin de suivre les calculs sans peine.

La seconde partie, sûrement la plus développée et la plus intéressantes, nous propose de suivre les raisonnements qui mèneront Boltzmann, Einstein puis Debye à proposer successivement des modèles de plus en plus fins afin d’expliquer le comportement de la chaleur spécifique des solides.

---

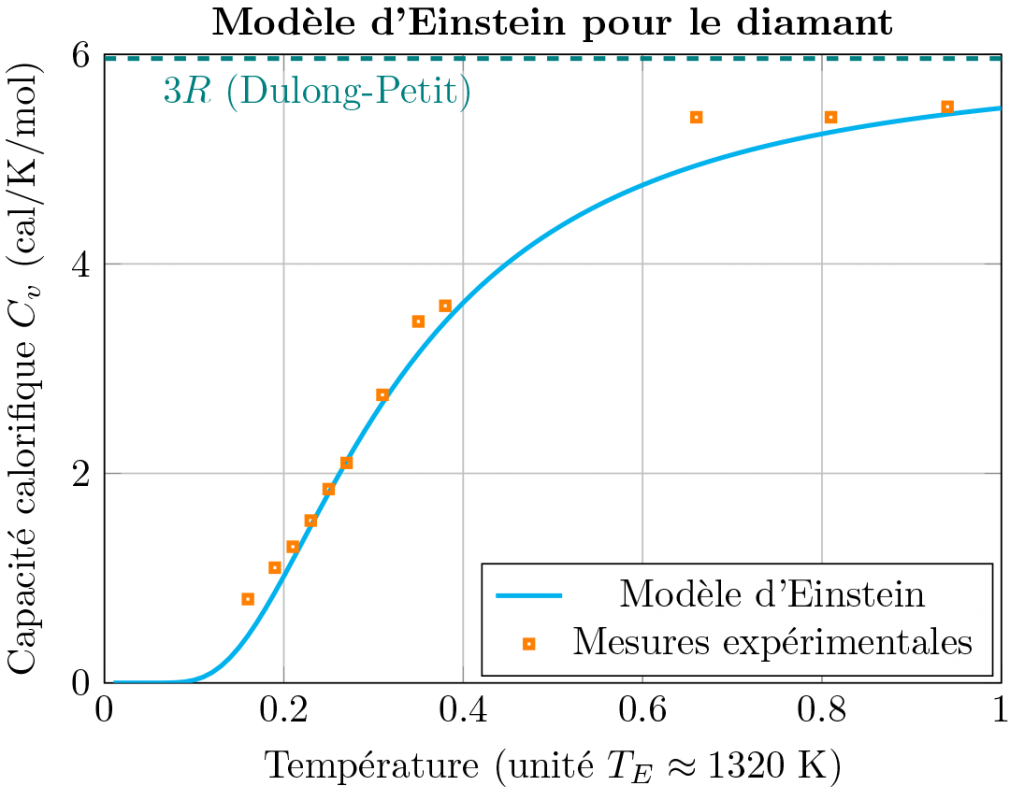
Alors que la loi de Dulong-Petit indique que la chaleur spécifique pour un solide est constante et que l’on a

(1)  

les données expérimentales indiquent ce cela n’est pas toujours le cas, en particulier aux basses températures. Einstein sera le premier à offrir des éléments de réponses.

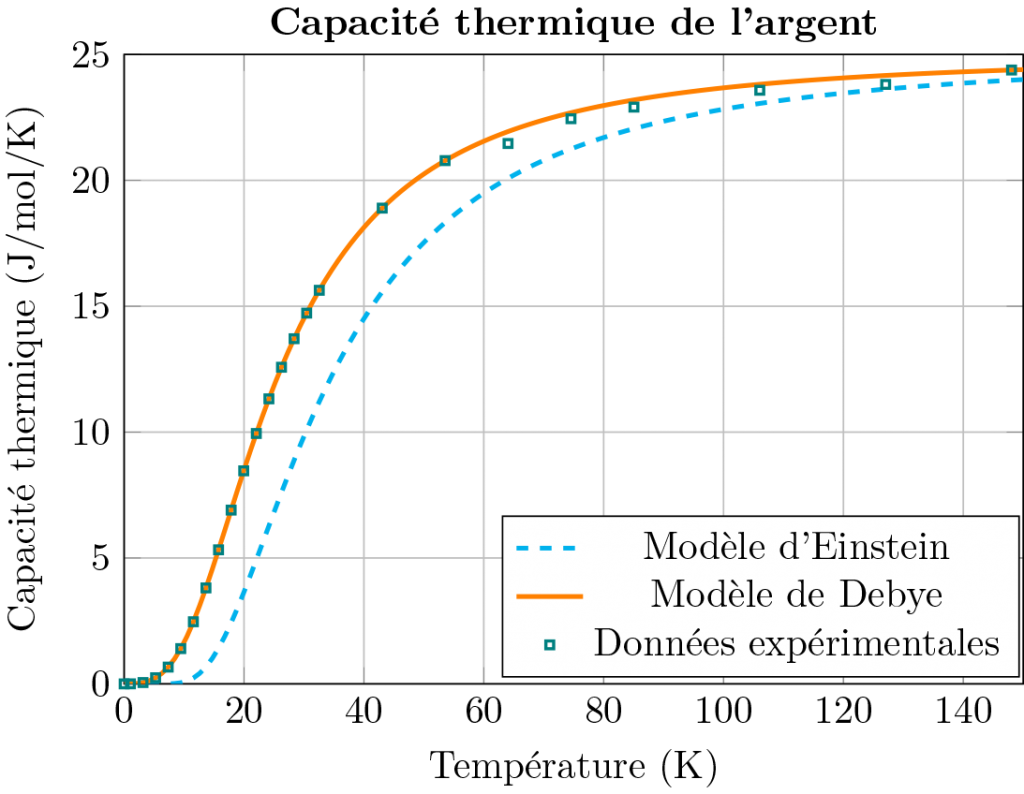
Debye parviendra à expliquer le comportement de la chaleurs spécifique à basse température, qui est alors proportionnelle à .

Le modèle d’Einstein n’est cependant pas parfait, et en ce sens, on peut voir que pour le diamant, les données expérimentales s’éloignent des valeurs théoriques. Ces écarts ne sont en réalité pas dus à des erreurs de mesures.

---

On peut constater que pour l’argent, les données expérimentales correspondent parfaitement à celles du modèle de Debye. En réalité, ce modèle a ses limites, en particulier aux très basses températures, pour les métaux, où la capacité thermique est alors proportionnelle à .

Enfin, la troisième et dernière partie se propose d’expliquer de manière succincte le phénomène de condensation de Bose-Einstein et en particulier l’apparition d’une température critique, sous certaines conditions, amenant à la formation de cet état particulier de la matière.

Conclusion :
Ce rapport d’une cinquantaine de pages contient de nombreuses informations qui peuvent se révéler utiles si l’on désire obtenir un premier aperçu des phénomènes sus-cités. Néanmoins, l’étude des ouvrages cités en référence se montrera indispensable si l’on souhaite bien comprendre les mécanismes mis en jeux ou tout simplement aller plus loin.